
Area and volume of the sphere |

Name: ______________________________________ Subject: _______________________ Date: _______
Write on the right side what is missing.
1. Sphere parts
In the picture we see several spherical objects: a globe, a balloon and a ball.

In the sphere, all points of the surface are at the same distance of an inner point called center.
The radius of the sphere is any line segment joining the center to a point on the spherical area. All radius of the sphere are equal.
Diameter is any segment that passes through the center and connects two points on the surface.
Look at this figure and answer:
1. The segment BO is a... |
|
2. The point O is... |
|
3. The segment AC is a... |
2. Area of the sphere
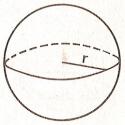
If we make a section through the center of the sphere, the circle that we obtain is called maximum circle because it is the maximum possible. The area of the spherical surface is equal to four maximum circles. The area of the circle is p x r2.
Area of the sphere = 4 x p x r2
Do these problems on a paper and answer:
1. Find the area m2 of a sphere of 1 m radius. |
|
2. Calculate the area m2 of a sphere of 0.8 m diameter. |
|
3. Find the area in cm2 of a sphere whose maximum circumference is 47.1 cm. |
|
4. Calculate in km2 the land area, if the radius of the Earth is 6370 km. |
3. Volume of the sphere
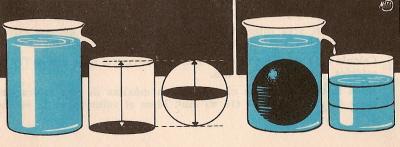
We fill a glass with water. Then we introduce a sphere and the displaced water falls into a cylindrical vessel that has the same base diameter and the same height as the sphere. We check that the glass is filled to the 2/3 of its height.
The volume of the cylinder is: p x r2 x 2 x r = 2 x p x r3
The volume of a sphere = 2/3 x 2 x p x r3 = 4/3 x p x r3
Do these problems on a paper and answer:
1. Find the volume in m3 of a sphere of 1 m radius. |
|
2. Calculate the volume in m3 of a sphere of 0.8 m diameter. |
|
3. Find the volume in cm3 of a sphere whose maximum circumference is 47.1 cm. |
|
4. Calculate the volume in cm3 of a sphere of 14 cm diameter. |
| Educational applications | Mathematics |
In Spanish | Interactive
®Arturo Ramo García.-Record of intellectual property of Teruel (Spain)
No 141, of 29-IX-1999
Plaza Playa de Aro, 3, 1º DO 44002-TERUEL