
Surface Area and volume of the prism |

Name: ______________________________________ Subject: _______________________ Date: _______
Write on the right side what is missing.
1. Surface area of the prism
We see that this hexagonal prism has 6 lateral faces that are rectangles and 2 bases that are hexagons.
The lateral area of a prism is the sum of the areas of its lateral faces (6 rectangles).
The 6 lateral faces form a rectangle whose base is the perimeter of the hexagon of the base. Therefore, the lateral area of the prism is equal to the product of the perimeter of the base times the height.
Lateral area = perimeter of the base x height.
The total area is the sum of the lateral area plus the area of the two bases.
You can see how to do
problems.
Answer these problems:
1. The dimensions of a rectangular parallelepiped are 4 m and 3 m base and 7 m height. Find the lateral area in m2 |
|
2. Find the surface area of the previous parallelepiped in m2 |
|
3. Find the lateral area in m2 of a triangular prism that has as base a right triangle whose legs are 3 m and 4 m and its hypotenuse is 5 m. its height is 6 m. |
|
Find the surface area of the previous triangular prism in m2 |
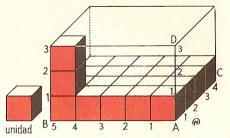
2. Volume of prism
The rectangular prism of the picture is 5 cm length, 4 cm wide and 3 cm height. In the first layer, there are 5 x 4 cm2. As it has 3 layers, the number of cm3 will be 20 x 3 = 60 cm3.
The rectangular prism volume is the product of its three dimensions. In general, the volume of any prism is equal to the product of the area of the base times the height.
Do these problems on a paper and answer:
1. Find the volume of a prism whose height is 5 m and the base is a rhombus whose diagonals are 6 m and 8 m. |
|
2. Calculate the volume of a pentagonal prism with 27 m2 base and 72 m height. |
|
3. Find the volume in m3 of a triangular prism that has as base a right triangle whose legs are 3 and 4 meters and 6 m height. |
|
4. Find the lateral area in m2 of a triangular prism of 2.24 m height and whose base is 3.75 m in perimeter. |
| Educational applications | Mathematics |
In Spanish | Interactive
®Arturo Ramo García.-Record of intellectual property of Teruel (Spain)
No 141, of 29-IX-1999
Plaza Playa de Aro, 3, 1º DO 44002-TERUEL